Algorytmy i struktury danych - Drzewa
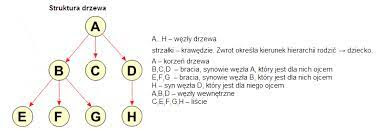
1. Drzewo jest strukturą danych zbudowaną z elementów, które nazywamy węzłami. Dane przechowuje się w węzłach drzewa. Węzły są ze sobą powiązane w sposób hierarchiczny za pomocą krawędzi, które zwykle przedstawia się za pomocą strzałki określającej hierarchię. Pierwszy węzeł drzewa nazywa się korzeniem. Od niego "wyrastają" pozostałe węzły, które będziemy nazywać synami. Synowie są węzłami podrzędnymi w strukturze hierarchicznej. Synowie tego samego ojca są nazywani braćmi. Węzeł nadrzędny w stosunku do syna nazwiemy ojcem. Ojcowie są węzłami nadrzędnymi w strukturze hierarchicznej. Jeśli węzeł nie posiada synów, to nazywa się liściem, w przeciwnym razie nazywa się węzłem wewnętrznym. Droga od korzenia do liścia nazywana jest gałęzią. Wysokość węzła to długość najdłużej ścieżki od węzła do liścia. Wysokość drzewa to wysokość korzenia. Głębokością węzła w drzewie jest długość ścieżki od korzenia do tego węzła.
2. Drzewo, w którym węzły mogą posiadać co najwyżej dwóch synów, nazywa się drzewem binarnym. Przechodzenie wierzchołków drzewa binarnego w kolejności DFS (w głąb):
- preorder (odwiedź korzeń, przejdź lewe poddrzewo, przejdź prawe poddrzewo)
- postorder (przejdź lewe poddrzewo, przejdź prawe poddrzewo, odwiedź korzeń)
- inorder (przejdź lewe poddrzewo, odwiedź korzeń, przejdź prawe poddrzewo)
4. Następnik – następny węzeł odwiedzany w czasie przechodzenia drzewa w porządku
inorder
5. Drzewo doskonale zrównoważone – dla dowolnego wierzchołka rozmiar lewego i
prawego poddrzewa różnią się najwyżej o 1.
6. Drzewo zrównoważone – długość dowolnej ścieżki z węzła do liści różni się od
wysokości tego węzła najwyżej o 1.
Drzewo AVL nazywane również drzewem dopuszczalnym, to zrównoważone binarne
drzewo poszukiwań (BST), w którym wysokość lewego i prawego poddrzewa każdego
węzła różni się co najwyżej o jeden.
7. Drzewo w przybliżeniu zrównoważone – długość dowolnej ścieżki z węzła do liści różni
się od wysokości tego węzła najwyżej 2 razy.
8. Drzewo czerwono-czarne jest drzewem wyszukiwań binarnych, w którym każdy węzeł
zawiera dodatkowy bit informacji: kolor oraz każdy węzeł jest czerwony albo czarny; korzeń jest czarny; każdy liść jest czarny; jeżeli węzeł jest czerwony, to obaj jego synowie są czarni; każda ścieżka z ustalonego węzła do liścia ma tyle samo czarnych węzłów.
9. Kopiec inaczej zwany stogiem lub stertą jest szczególnym przypadkiem drzewa
binarnego, które spełnia warunek kopca (jeżeli w drzewie binarnym węzeł x jest synem węzła y, to
wartość klucza w węźle x nie jest większa od wartości klucza w węźle y).
Kopiec zupełny – to kopiec będący zupełnym drzewem binarnym. Drzewo binarne jest zupełne wtedy, gdy wszystkie poziomy z wyjątkiem ostatniego są całkowicie zapełnione, a na ostatnim poziomie liście są spójnie ułożone od strony lewej do prawej.